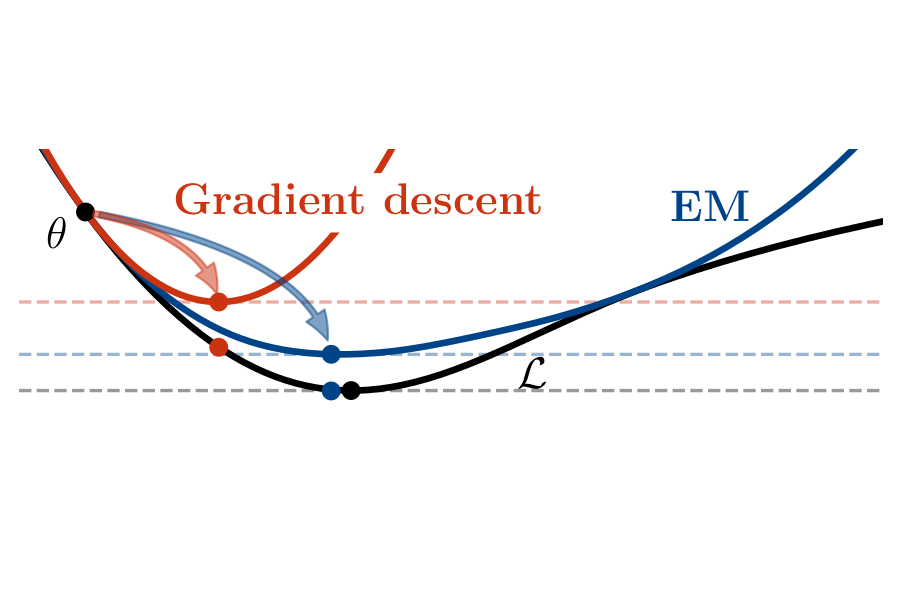
Expectation maximization (EM) is the default algorithm for fitting probabilistic models with missing or latent variables, yet we lack a full understanding of its non-asymptotic convergence properties. Previous works show results along the lines of "EM converges at least as fast as gradient descent" by assuming the conditions for the convergence of gradient descent apply to EM. This approach is not only loose, in that it does not capture that EM can make more progress than a gradient step, but the assumptions fail to hold for textbook examples of EM like Gaussian mixtures. In this work we first show that for the common setting of exponential family distributions, viewing EM as a mirror descent algorithm leads to convergence rates in Kullback-Leibler (KL) divergence. Then, we show how the KL divergence is related to first-order stationarity via Bregman divergences. In contrast to previous works, the analysis is invariant to the choice of parametrization and holds with minimal assumptions. We also show applications of these ideas to local linear (and superlinear) convergence rates, generalized EM, and non-exponential family distributions.

Gaussian processes are a versatile framework for learning unknown functions in a manner that permits one to utilize prior information about their properties. Although many different Gaussian process models are readily available when the input space is Euclidean, the choice is much more limited for Gaussian processes whose input space is an undirected graph. In this work, we leverage the stochastic partial differential equation characterization of Matérn Gaussian processes—a widely-used model class in the Euclidean setting—to study their analog for undirected graphs. We show that the resulting Gaussian processes inherit various attractive properties of their Euclidean and Riemannian analogs and provide techniques that allow them to be trained using standard methods, such as inducing points. This enables graph Matérn Gaussian processes to be employed in mini-batch and non-conjugate settings, thereby making them more accessible to practitioners and easier to deploy within larger learning frameworks.