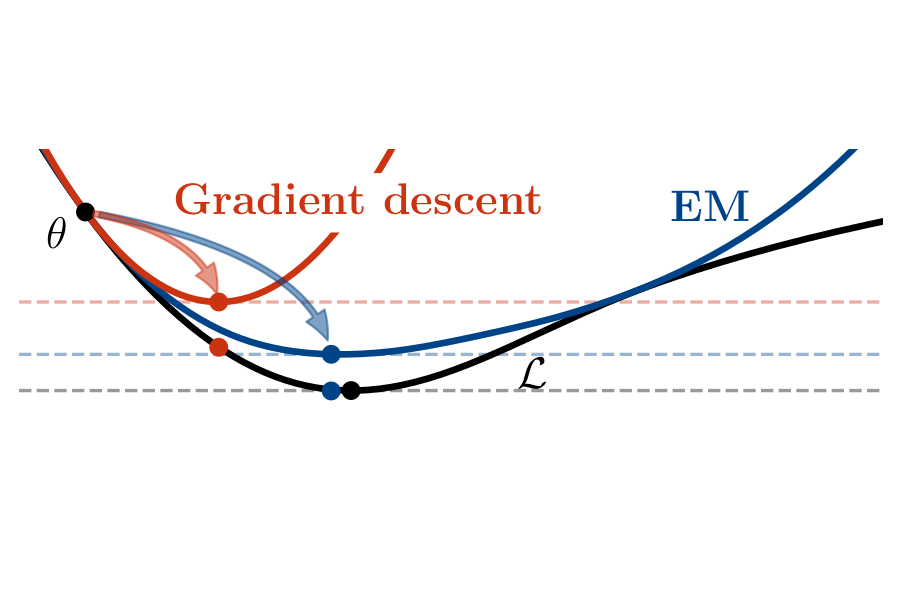
Expectation maximization (EM) is the default algorithm for fitting probabilistic models with missing or latent variables, yet we lack a full understanding of its non-asymptotic convergence properties. Previous works show results along the lines of "EM converges at least as fast as gradient descent" by assuming the conditions for the convergence of gradient descent apply to EM. This approach is not only loose, in that it does not capture that EM can make more progress than a gradient step, but the assumptions fail to hold for textbook examples of EM like Gaussian mixtures. In this work we first show that for the common setting of exponential family distributions, viewing EM as a mirror descent algorithm leads to convergence rates in Kullback-Leibler (KL) divergence. Then, we show how the KL divergence is related to first-order stationarity via Bregman divergences. In contrast to previous works, the analysis is invariant to the choice of parametrization and holds with minimal assumptions. We also show applications of these ideas to local linear (and superlinear) convergence rates, generalized EM, and non-exponential family distributions.

Despite the ubiquity of kernel-based clustering, surprisingly few statistical guarantees exist beyond settings that consider strong structural assumptions on the data generation process. In this work, we take a step towards bridging this gap by studying the statistical performance of kernel-based clustering algorithms under non-parametric mixture models. We provide necessary and sufficient separability conditions under which these algorithms can consistently recover the underlying true clustering. Our analysis provides guarantees for kernel clustering approaches without structural assumptions on the form of the component distributions. Additionally, we establish a key equivalence between kernel-based data-clustering and kernel density-based clustering. This enables us to provide consistency guarantees for kernel-based estimators of non-parametric mixture models. Along with theoretical implications, this connection could have practical implications, including in the systematic choice of the bandwidth of the Gaussian kernel in the context of clustering.

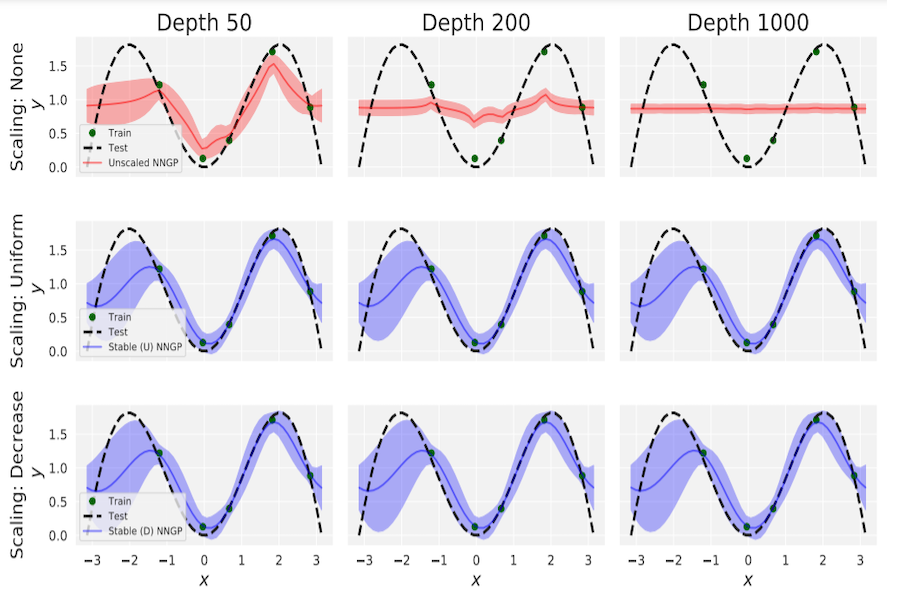
Deep ResNet architectures have achieved state of the art performance on many tasks. While they solve the problem of gradient vanishing, they might suffer from gradient exploding as the depth becomes large (Yang et al. 2017). Moreover, recent results have shown that ResNet might lose expressivity as the depth goes to infinity (Yang et al. 2017, Hayou et al. 2019). To resolve these issues, we introduce a new class of ResNet architectures, calledStable ResNet, that have the property of stabilizing the gradient while ensuring expressivity in the infinite depth limit.

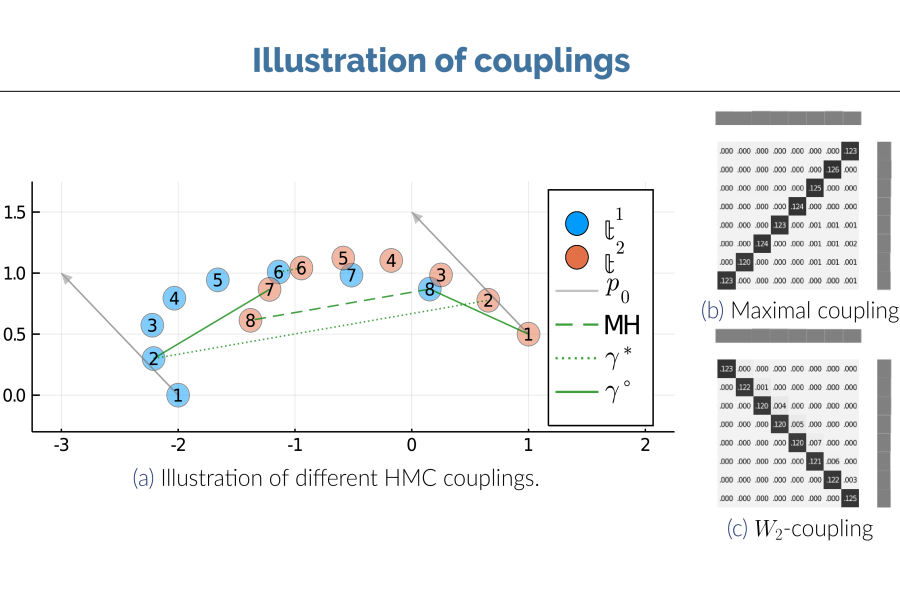
Hamiltonian Monte Carlo (HMC) is a popular sampling method in Bayesian inference. Recently, Heng & Jacob (2019) studied Metropolis HMC with couplings for unbiased Monte Carlo estimation, establishing a generic parallelizable scheme for HMC. However, in practice a different HMC method, multinomial HMC, is considered as the go-to method, e.g. as part of the no-U-turn sampler. In multinomial HMC, proposed states are not limited to end-points as in Metropolis HMC; instead points along the entire trajectory can be proposed. In this paper, we establish couplings for multinomial HMC, based on optimal transport for multinomial sampling in its transition. We prove an upper bound for the meeting time -- the time it takes for the coupled chains to meet -- based on the notion of local contractivity. We evaluate our methods using three targets: 1,000 dimensional Gaussians, logistic regression and log-Gaussian Cox point processes. Compared to Heng & Jacob (2019), coupled multinomial HMC generally attains a smaller meeting time, and is more robust to choices of step sizes and trajectory lengths, which allows re-use of existing adaptation methods for HMC. These improvements together paves the way for a wider and more practical use of coupled HMC methods.

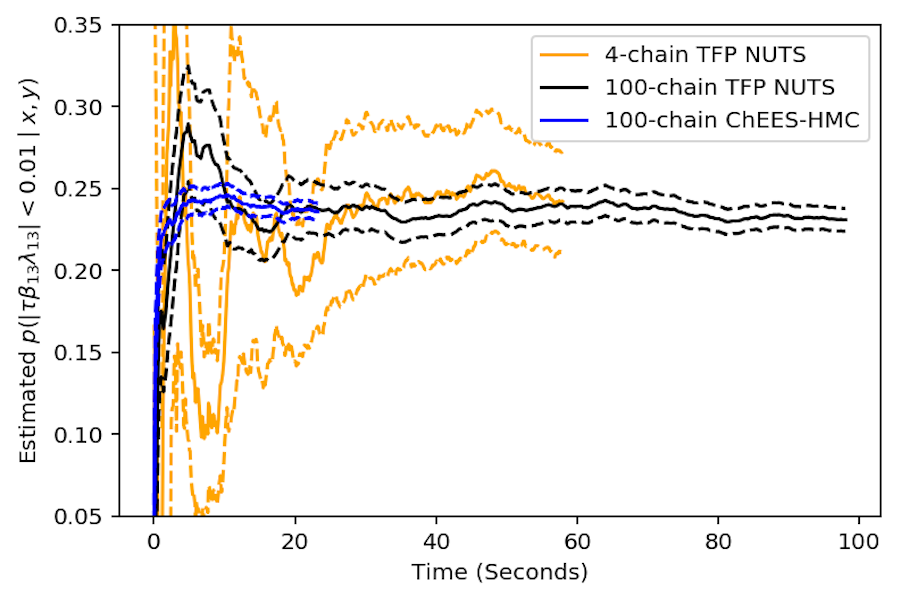
Hamiltonian Monte Carlo (HMC) is a powerful MCMC algorithm based on simulating Hamiltonian dynamics. Its performance depends strongly on choosing appropriate values for two parameters: the step size used in the simulation, and how long the simulation runs for. The step-size parameter can be tuned using standard adaptive-MCMC strategies, but it is less obvious how to tune the simulation-length parameter. The no-U-turn sampler (NUTS) eliminates this problematic simulation-length parameter, but NUTS’s relatively complex control flow makes it difficult to efficiently run many parallel chains on accelerators such as GPUs. NUTS also spends some extra gradient evaluations relative to HMC in order to decide how long to run each iteration without violating detailed balance. We propose ChEES-HMC, a simple adaptive-MCMC scheme for automatically tuning HMC’s simulation-length parameter, which minimizes a proxy for the autocorrelation of the state’s second moments. We evaluate ChEES-HMC and NUTS on many tasks, and find that ChEES-HMC typically yields larger effective sample sizes per gradient evaluation than NUTS does. When running many chains on a GPU, ChEES-HMC can also run significantly more gradient evaluations per second than NUTS, allowing it to quickly provide accurate estimates of posterior expectations.

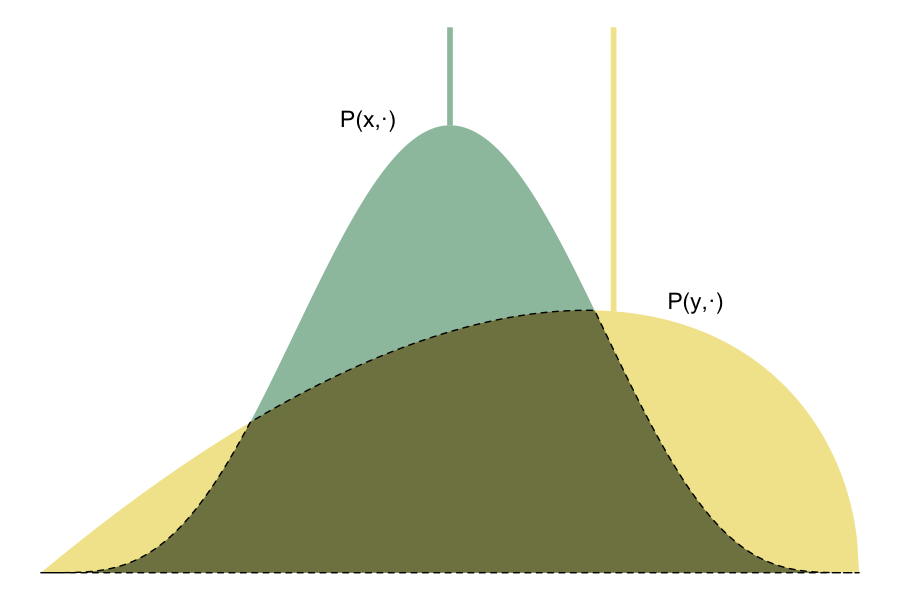
Couplings play a central role in the analysis of Markov chain Monte Carlo algorithms and appear increasingly often in the algorithms themselves, e.g. in convergence diagnostics, parallelization, and variance reduction techniques. Existing couplings of the Metropolis-Hastings algorithm handle the proposal and acceptance steps separately and fall short of the upper bound on one-step meeting probabilities given by the coupling inequality. This paper introduces maximal couplings which achieve this bound while retaining the practical advantages of current methods. We consider the properties of these couplings and examine their behavior on a selection of numerical examples.

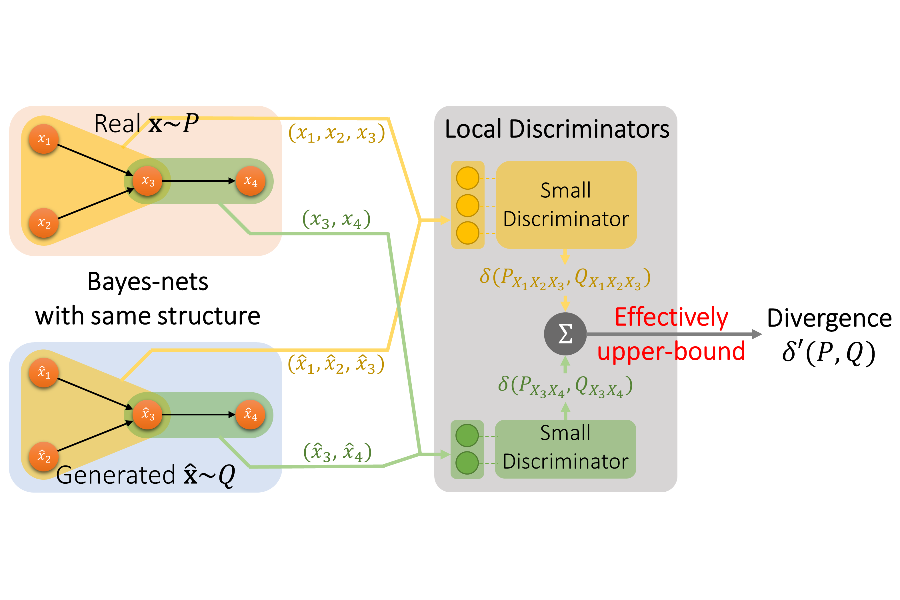
Generative Adversarial Networks (GANs) are modern methods to learn the underlying distribution of a data set. GANs have been widely used in sample synthesis, de-noising, domain transfer, etc. GANs, however, are designed in a model-free fashion where no additional information about the underlying distribution is available. In many applications, however, practitioners have access to the underlying independence graph of the variables, either as a Bayesian network or a Markov Random Field (MRF). We ask: how can one use this additional information in designing model-based GANs? In this paper, we provide theoretical foundations to answer this question by studying subadditivity properties of probability divergences, which establish upper bounds on the distance between two high-dimensional distributions by the sum of distances between their marginals over (local) neighborhoods of the graphical structure of the Bayes-net or the MRF. We prove that several popular probability divergences satisfy some notion of subadditivity under mild conditions. These results lead to a principled design of a model-based GAN that uses a set of simple discriminators on the neighborhoods of the Bayes-net/MRF, rather than a giant discriminator on the entire network, providing significant statistical and computational benefits. Our experiments on synthetic and real-world datasets demonstrate the benefits of …

A general framework of personalized federated multi-armed bandits (PF-MAB) is proposed, which is a new bandit paradigm analogous to the federated learning (FL) framework in supervised learning and enjoys the features of FL with personalization. Under the PF-MAB framework, a mixed bandit learning problem that flexibly balances generalization and personalization is studied. A lower bound analysis for the mixed model is presented. We then propose the Personalized Federated Upper Confidence Bound (PF-UCB) algorithm, where the exploration length is chosen carefully to achieve the desired balance of learning the local model and supplying global information for the mixed learning objective. Theoretical analysis proves that PF-UCB achieves an O(log(T)) regret regardless of the degree of personalization, and has a similar instance dependency as the lower bound. Experiments using both synthetic and real-world datasets corroborate the theoretical analysis and demonstrate the effectiveness of the proposed algorithm.

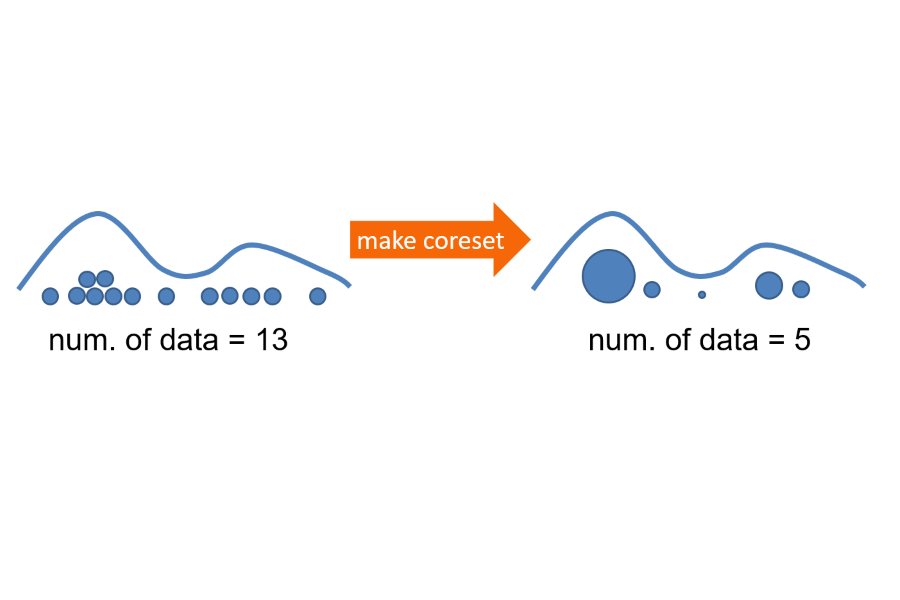
Bayesian coresets have emerged as a promising approach for implementing scalable Bayesian inference. The Bayesian coreset problem involves selecting a (weighted) subset of the data samples, such that the posterior inference using the selected subset closely approximates the posterior inference using the full dataset. This manuscript revisits Bayesian coresets through the lens of sparsity constrained optimization. Leveraging recent advances in accelerated optimization methods, we propose and analyze a novel algorithm for coreset selection. We provide explicit convergence rate guarantees and present an empirical evaluation on a variety of benchmark datasets to highlight our proposed algorithm's superior performance compared to state-of-the-art on speed and accuracy.

Optimal transport (OT) theory provides powerful tools to compare probability measures. However, OT is limited to nonnegative measures having the same mass, and suffers serious drawbacks about its computation and statistics. This leads to several proposals of regularized variants of OT in the recent literature. In this work, we consider an entropy partial transport (EPT) problem for nonnegative measures on a tree having different masses. The EPT is shown to be equivalent to a standard complete OT problem on a one-node extended tree. We derive its dual formulation, then leverage this to propose a novel regularization for EPT which admits fast computation and negative definiteness. To our knowledge, the proposed regularized EPT is the first approach that yields a closed-form solution among available variants of unbalanced OT for general nonnegative measures. For practical applications without prior knowledge about the tree structure for measures, we propose tree-sliced variants of the regularized EPT, computed by averaging the regularized EPT between these measures using random tree metrics, built adaptively from support data points. Exploiting the negative definiteness of our regularized EPT, we introduce a positive definite kernel, and evaluate it against other baselines on benchmark tasks such as document classification with word embedding …

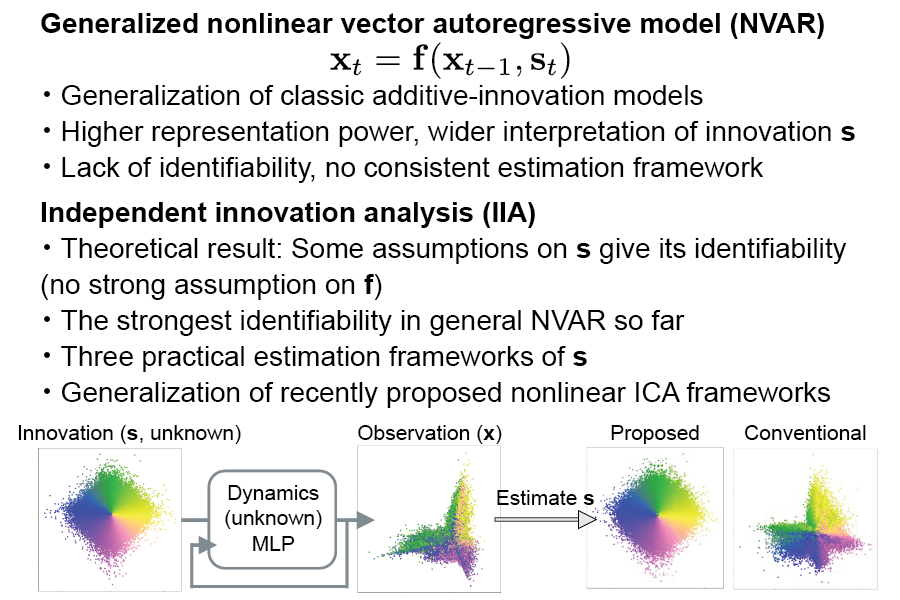
The nonlinear vector autoregressive (NVAR) model provides an appealing framework to analyze multivariate time series obtained from a nonlinear dynamical system. However, the innovation (or error), which plays a key role by driving the dynamics, is almost always assumed to be additive. Additivity greatly limits the generality of the model, hindering analysis of general NVAR processes which have nonlinear interactions between the innovations. Here, we propose a new general framework called independent innovation analysis (IIA), which estimates the innovations from completely general NVAR. We assume mutual independence of the innovations as well as their modulation by an auxiliary variable (which is often taken as the time index and simply interpreted as nonstationarity). We show that IIA guarantees the identifiability of the innovations with arbitrary nonlinearities, up to a permutation and component-wise invertible nonlinearities. We also propose three estimation frameworks depending on the type of the auxiliary variable. We thus provide the first rigorous identifiability result for general NVAR, as well as very general tools for learning such models.

While uncertainty estimation is a well-studied topic in deep learning, most such work focuses on marginal uncertainty estimates, i.e. the predictive mean and variance at individual input locations. But it is often more useful to estimate predictive correlations between the function values at different input locations. In this paper, we consider the problem of benchmarking how accurately Bayesian models can estimate predictive correlations. We first consider a downstream task which depends on posterior predictive correlations: transductive active learning (TAL). We find that TAL makes better use of models' uncertainty estimates than ordinary active learning, and recommend this as a benchmark for evaluating Bayesian models. Since TAL is too expensive and indirect to guide development of algorithms, we introduce two metrics which more directly evaluate the predictive correlations and which can be computed efficiently: meta-correlations (i.e. the correlations between the models correlation estimates and the true values), and cross-normalized likelihoods (XLL). We validate these metrics by demonstrating their consistency with TAL performance and obtain insights about the relative performance of current Bayesian neural net and Gaussian process models.

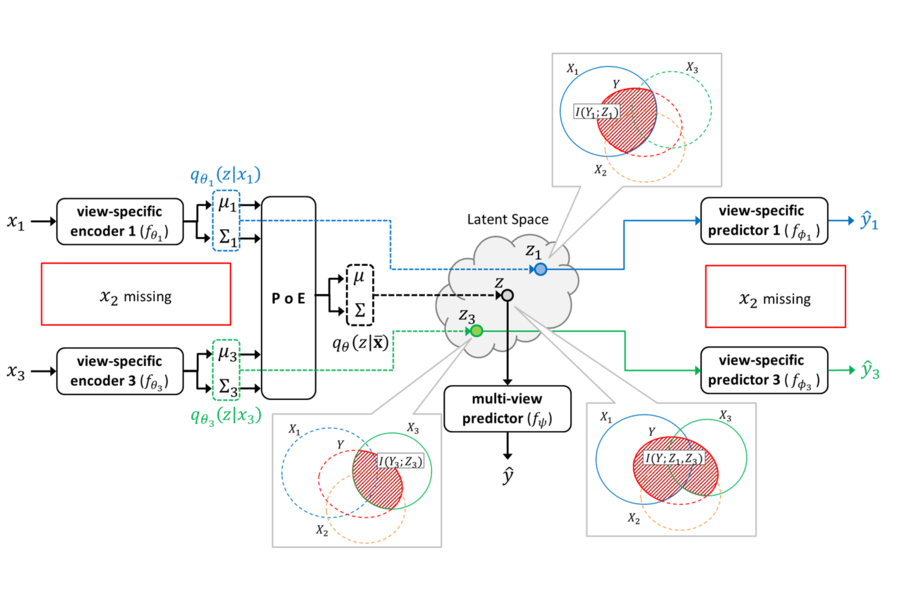
Integration of data from multiple omics techniques is becoming increasingly important in biomedical research. Due to non-uniformity and technical limitations in omics platforms, such integrative analyses on multiple omics, which we refer to as views, involve learning from incomplete observations with various view-missing patterns. This is challenging because i) complex interactions within and across observed views need to be properly addressed for optimal predictive power and ii) observations with various view-missing patterns need to be flexibly integrated. To address such challenges, we propose a deep variational information bottleneck (IB) approach for incomplete multi-view observations. Our method applies the IB framework on marginal and joint representations of the observed views to focus on intra-view and inter-view interactions that are relevant for the target. Most importantly, by modeling the joint representations as a product of marginal representations, we can efficiently learn from observed views with various view-missing patterns. Experiments on real-world datasets show that our method consistently achieves gain from data integration and outperforms state-of-the-art benchmarks.

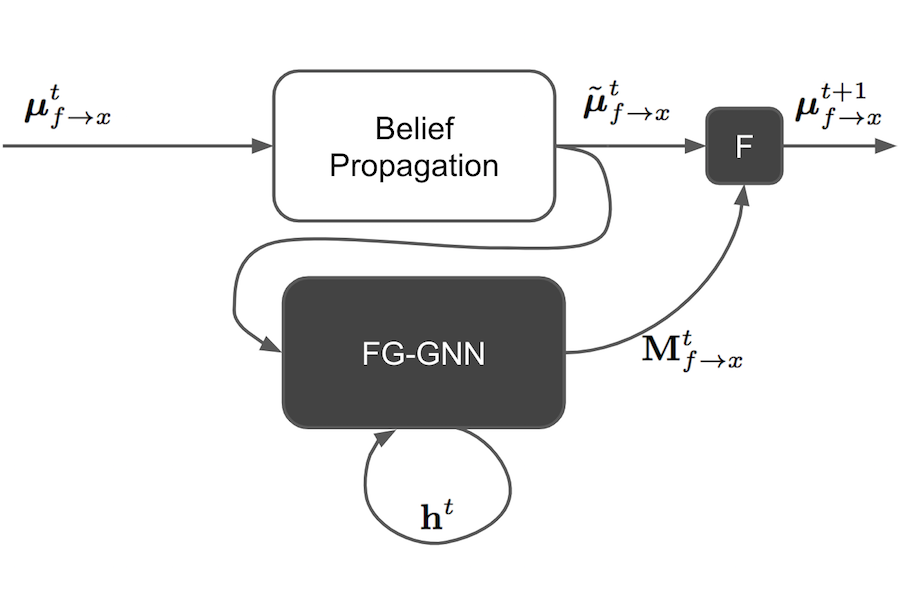
A graphical model is a structured representation of locally dependent random variables. A traditional method to reason over these random variables is to perform inference using belief propagation. When provided with the true data generating process, belief propagation can infer the optimal posterior probability estimates in tree structured factor graphs. However, in many cases we may only have access to a poor approximation of the data generating process, or we may face loops in the factor graph, leading to suboptimal estimates. In this work we first extend graph neural networks to factor graphs (FG-GNN). We then propose a new hybrid model that runs conjointly a FG-GNN with belief propagation. The FG-GNN receives as input messages from belief propagation at every inference iteration and outputs a corrected version of them. As a result, we obtain a more accurate algorithm that combines the benefits of both belief propagation and graph neural networks. We apply our ideas to error correction decoding tasks, and we show that our algorithm can outperform belief propagation for LDPC codes on bursty channels.

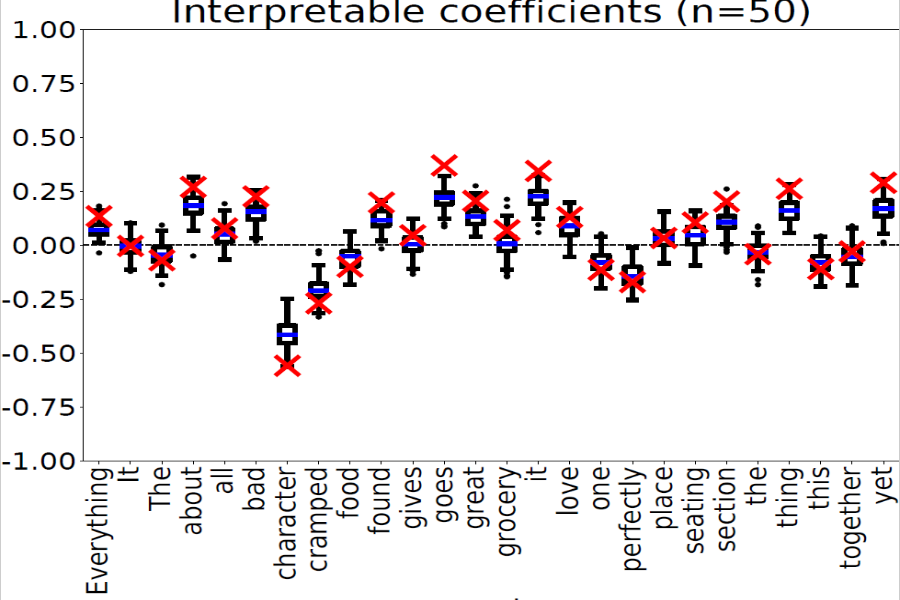
Text data are increasingly handled in an automated fashion by machine learning algorithms. But the models handling these data are not always well-understood due to their complexity and are more and more often referred to as ``black-boxes.'' Interpretability methods aim to explain how these models operate. Among them, LIME has become one of the most popular in recent years. However, it comes without theoretical guarantees: even for simple models, we are not sure that LIME behaves accurately. In this paper, we provide a first theoretical analysis of LIME for text data. As a consequence of our theoretical findings, we show that LIME indeed provides meaningful explanations for simple models, namely decision trees and linear models.

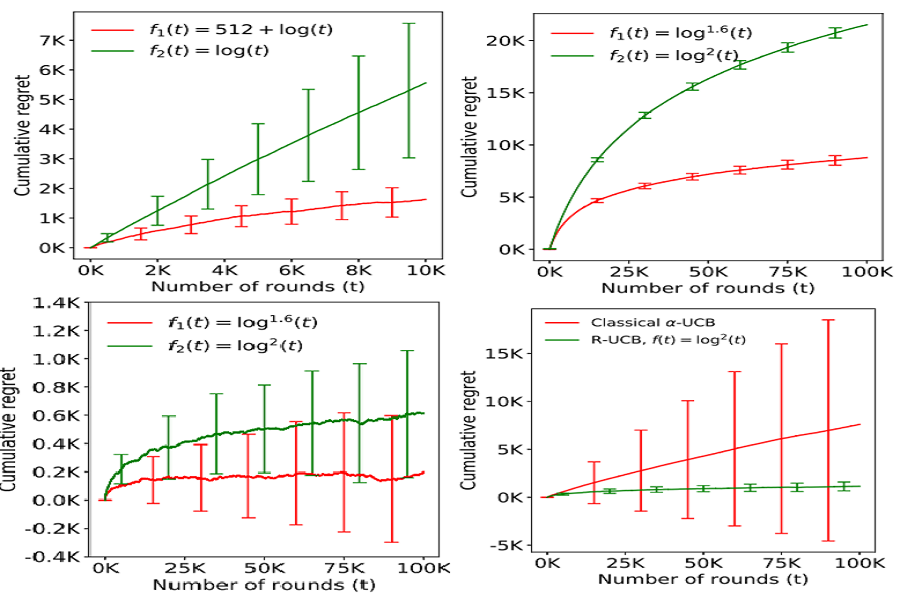
We study regret minimization in a stochastic multi-armed bandit setting, and establish a fundamental trade-off between the regret suffered under an algorithm, and its statistical robustness. Considering broad classes of underlying arms' distributions, we show that bandit learning algorithms with logarithmic regret are always inconsistent and that consistent learning algorithms always suffer a super-logarithmic regret. This result highlights the inevitable statistical fragility of all `logarithmic regret' bandit algorithms available in the literature - for instance, if a UCB algorithm designed for 1-subGaussian distributions is used in a subGaussian setting with a mismatched variance parameter, the learning performance could be inconsistent. Next, we show a positive result: statistically robust and consistent learning performance is attainable if we allow the regret to be slightly worse than logarithmic. Specifically, we propose three classes of distribution oblivious algorithms that achieve an asymptotic regret that is arbitrarily close to logarithmic.

We study the problem of approximating the level set of an unknown function by sequentially querying its values. We introduce a family of algorithms called Bisect and Approximate through which we reduce the level set approximation problem to a local function approximation problem. We then show how this approach leads to rate-optimal sample complexity guarantees for Hölder functions, and we investigate how such rates improve when additional smoothness or other structural assumptions hold true.

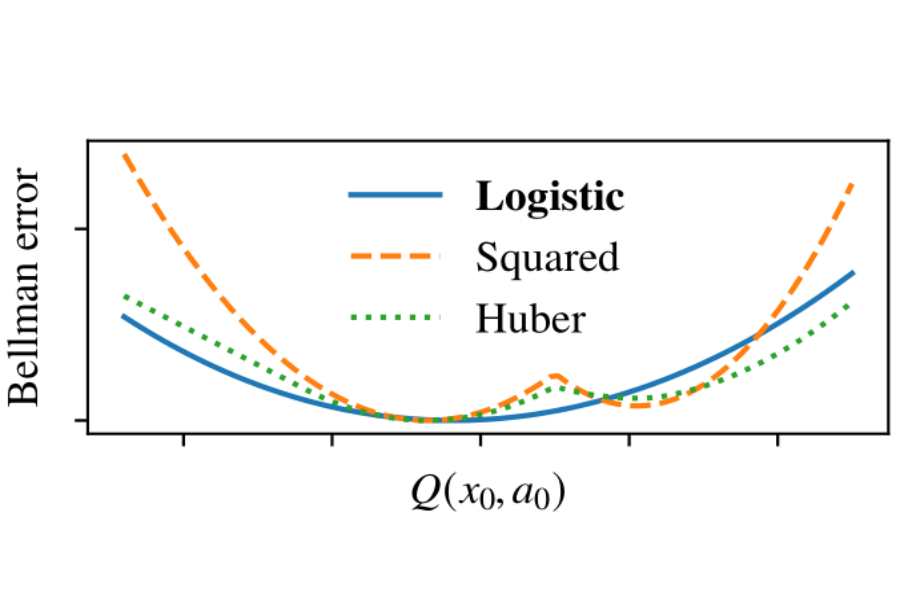
We propose a new reinforcement learning algorithm derived from a regularized linear-programming formulation of optimal control in MDPs. The method is closely related to the classic Relative Entropy Policy Search (REPS) algorithm of Peters et al. (2010), with the key difference that our method introduces a Q-function that enables efficient exact model-free implementation. The main feature of our algorithm (called QREPS) is a convex loss function for policy evaluation that serves as a theoretically sound alternative to the widely used squared Bellman error. We provide a practical saddle-point optimization method for minimizing this loss function and provide an error-propagation analysis that relates the quality of the individual updates to the performance of the output policy. Finally, we demonstrate the effectiveness of our method on a range of benchmark problems.

Domain generalization is the problem of machine learning when the training data and the test data come from different ``domains'' (data distributions). We propose an elementary theoretical model of the domain generalization problem, introducing the concept of a meta-distribution over domains. In our model, the training data available to a learning algorithm consist of multiple datasets, each from a single domain, drawn in turn from the meta-distribution. We show that our model can capture a rich range of learning phenomena specific to domain generalization for three different settings: learning with Massart noise, learning decision trees, and feature selection. We demonstrate approaches that leverage domain generalization to reduce computational or data requirements in each of these settings. Experiments demonstrate that our feature selection algorithm indeed ignores spurious correlations and improves generalization.

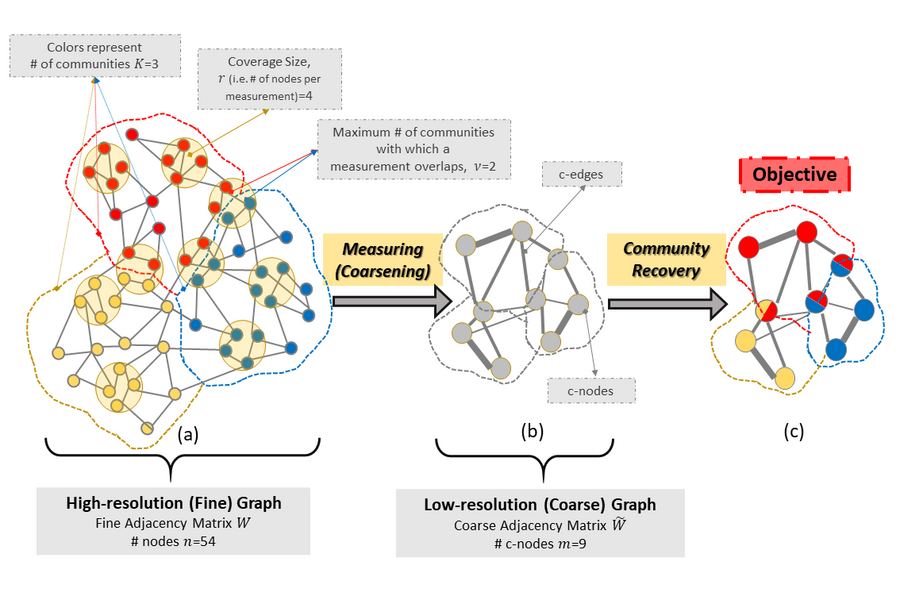
We study the problem of community recovery from coarse measurements of a graph. In contrast to the problem of community recovery of a fully observed graph, one often encounters situations when measurements of a graph are made at low-resolution, each measurement integrating across multiple graph nodes. Such low-resolution measurements effectively induce a coarse graph with its own communities. Our objective is to develop conditions on the graph structure, the quantity, and properties of measurements, under which we can recover the community organization in this coarse graph. In this paper, we build on the stochastic block model by mathematically formalizing the coarsening process, and characterizing its impact on the community members and connections. Accordingly, we characterize an error bound for community recovery. The error bound yields simple and closed-form asymptotic conditions to achieve the perfect recovery of the coarse graph communities.

Gaussian processes are a versatile framework for learning unknown functions in a manner that permits one to utilize prior information about their properties. Although many different Gaussian process models are readily available when the input space is Euclidean, the choice is much more limited for Gaussian processes whose input space is an undirected graph. In this work, we leverage the stochastic partial differential equation characterization of Matérn Gaussian processes—a widely-used model class in the Euclidean setting—to study their analog for undirected graphs. We show that the resulting Gaussian processes inherit various attractive properties of their Euclidean and Riemannian analogs and provide techniques that allow them to be trained using standard methods, such as inducing points. This enables graph Matérn Gaussian processes to be employed in mini-batch and non-conjugate settings, thereby making them more accessible to practitioners and easier to deploy within larger learning frameworks.

We consider learning a sparse pairwise Markov Random Field (MRF) with continuous-valued variables from i.i.d samples. We adapt the algorithm of Vuffray et al. (2019) to this setting and provide finite-sample analysis revealing sample complexity scaling logarithmically with the number of variables, as in the discrete and Gaussian settings. Our approach is applicable to a large class of pairwise MRFs with continuous variables and also has desirable asymptotic properties, including consistency and normality under mild conditions. Further, we establish that the population version of the optimization criterion employed in Vuffray et al. (2019) can be interpreted as local maximum likelihood estimation (MLE). As part of our analysis, we introduce a robust variation of sparse linear regression a` la Lasso, which may be of interest in its own right.

We study the problem of differentially private optimization with linear constraints when the right-hand-side of the constraints depends on private data. This type of problem appears in many applications, especially resource allocation. Previous research provided solutions that retained privacy but sometimes violated the constraints. In many settings, however, the constraints cannot be violated under any circumstances. To address this hard requirement, we present an algorithm that releases a nearly-optimal solution satisfying the constraints with probability 1. We also prove a lower bound demonstrating that the difference between the objective value of our algorithm's solution and the optimal solution is tight up to logarithmic factors among all differentially private algorithms. We conclude with experiments demonstrating that our algorithm can achieve nearly optimal performance while preserving privacy.

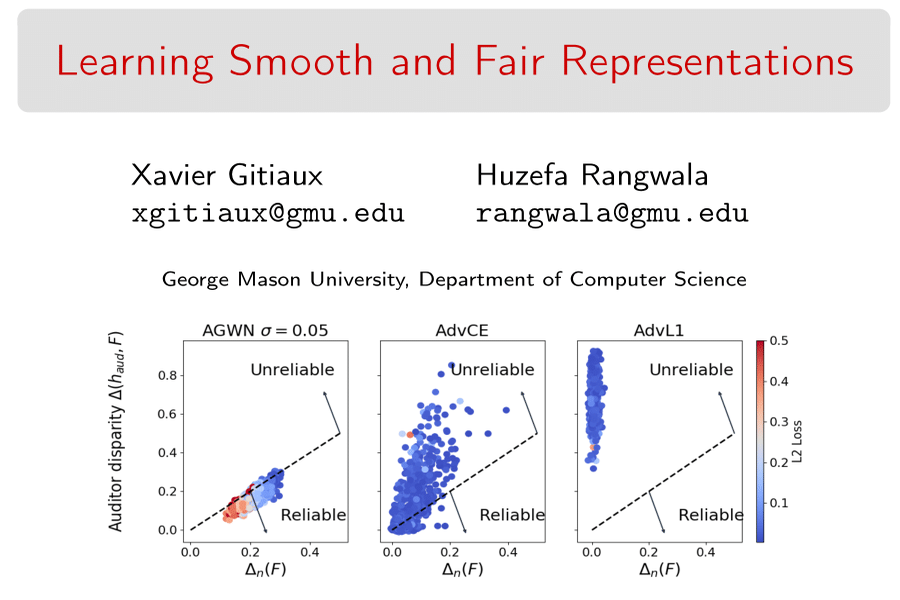
This paper explores the statistical properties of fair representation learning, a pre-processing method that preemptively removes the correlations between features and sensitive attributes by mapping features to a fair representation space. We show that the demographic parity of a representation can be certified from a finite sample if and only if the mapping guarantees that the chi-squared mutual information between features and representations is finite for distributions of the features. Empirically, we find that smoothing representations with an additive Gaussian white noise provides generalization guarantees of fairness certificates, which improves upon existing fair representation learning approaches.

Decision makers often need to rely on imperfect probabilistic forecasts. While average performance metrics are typically available, it is difficult to assess the quality of individual forecasts and the corresponding utilities. To convey confidence about individual predictions to decision-makers, we propose a compensation mechanism ensuring that the forecasted utility matches the actually accrued utility. While a naive scheme to compensate decision-makers for prediction errors can be exploited and might not be sustainable in the long run, we propose a mechanism based on fair bets and online learning that provably cannot be exploited. We demonstrate an application showing how passengers could confidently optimize individual travel plans based on flight delay probabilities estimated by an airline.

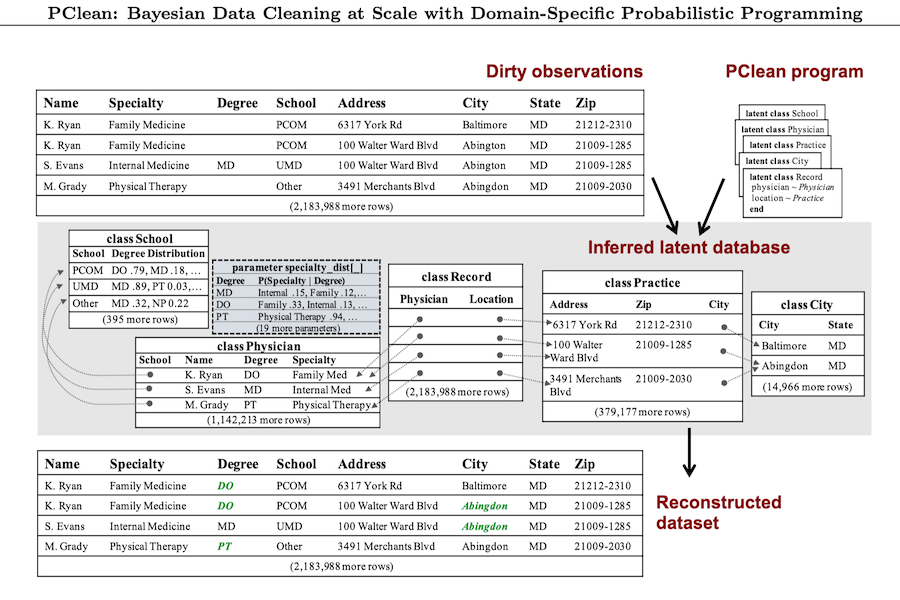
Data cleaning is naturally framed as probabilistic inference in a generative model of ground-truth data and likely errors, but the diversity of real-world error patterns and the hardness of inference make Bayesian approaches difficult to automate. We present PClean, a probabilistic programming language (PPL) for leveraging dataset-specific knowledge to automate Bayesian cleaning. Compared to general-purpose PPLs, PClean tackles a restricted problem domain, enabling three modeling and inference innovations: (1) a non-parametric model of relational database instances, which users' programs customize; (2) a novel sequential Monte Carlo inference algorithm that exploits the structure of PClean's model class; and (3) a compiler that generates near-optimal SMC proposals and blocked-Gibbs rejuvenation kernels based on the user's model and data. We show empirically that short (< 50-line) PClean programs can: be faster and more accurate than generic PPL inference on data-cleaning benchmarks; match state-of-the-art data-cleaning systems in terms of accuracy and runtime (unlike generic PPL inference in the same runtime); and scale to real-world datasets with millions of records.

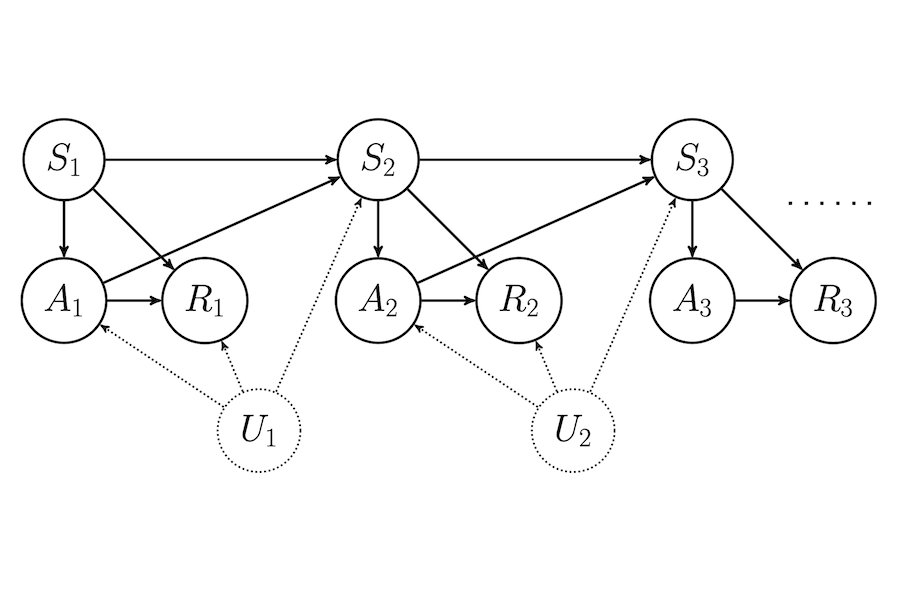
Off-policy evaluation (OPE) in reinforcement learning is an important problem in settings where experimentation is limited, such as healthcare. But, in these very same settings, observed actions are often confounded by unobserved variables making OPE even more difficult. We study an OPE problem in an infinite-horizon, ergodic Markov decision process with unobserved confounders, where states and actions can act as proxies for the unobserved confounders. We show how, given only a latent variable model for states and actions, policy value can be identified from off-policy data. Our method involves two stages. In the first, we show how to use proxies to estimate stationary distribution ratios, extending recent work on breaking the curse of horizon to the confounded setting. In the second, we show optimal balancing can be combined with such learned ratios to obtain policy value while avoiding direct modeling of reward functions. We establish theoretical guarantees of consistency and benchmark our method empirically.

We show that the Invariant Risk Minimization (IRM) formulation of Arjovsky et al. (2019) can fail to capture "natural" invariances, at least when used in its practical "linear" form, and even on very simple problems which directly follow the motivating examples for IRM. This can lead to worse generalization on new environments, even when compared to unconstrained ERM. The issue stems from a significant gap between the linear variant (as in their concrete method IRMv1) and the full non-linear IRM formulation. Additionally, even when capturing the "right" invariances, we show that it is possible for IRM to learn a sub-optimal predictor, due to the loss function not being invariant across environments. The issues arise even when measuring invariance on the population distributions, but are exacerbated by the fact that IRM is extremely fragile to sampling.

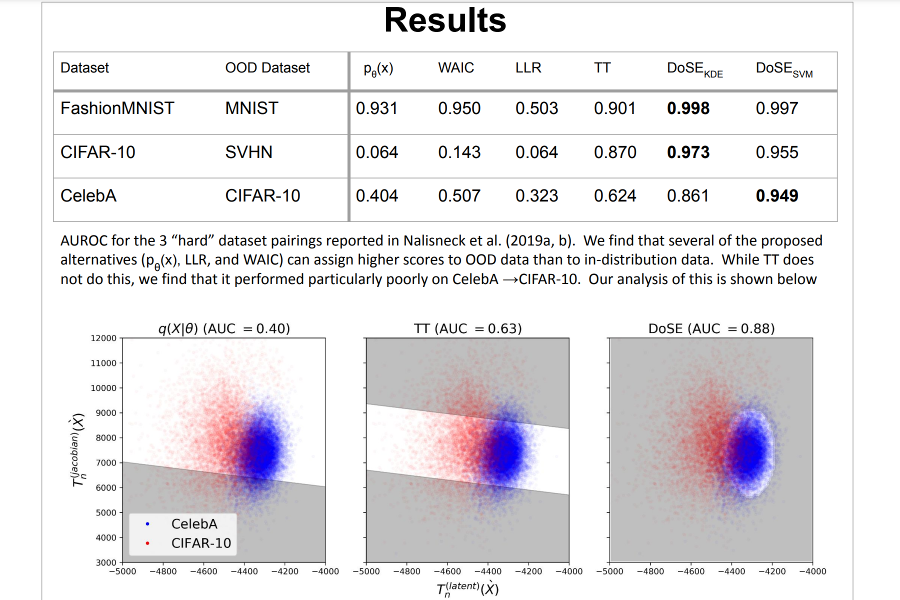
Perhaps surprisingly, recent studies have shown probabilistic model likelihoods have poor specificity for out-of-distribution (OOD) detection and often assign higher likelihoods to OOD data than in-distribution data. To ameliorate this issue we propose DoSE, the density of states estimator. Drawing on the statistical physics notion of density of states,'' the DoSE decision rule avoids direct comparison of model probabilities, and instead utilizes theprobability of the model probability,'' or indeed the frequency of any reasonable statistic. The frequency is calculated using nonparametric density estimators (e.g., KDE and one-class SVM) which measure the typicality of various model statistics given the training data and from which we can flag test points with low typicality as anomalous. Unlike many other methods, DoSE requires neither labeled data nor OOD examples. DoSE is modular and can be trivially applied to any existing, trained model. We demonstrate DoSE's state-of-the-art performance against other unsupervised OOD detectors on previously established ``hard'' benchmarks.

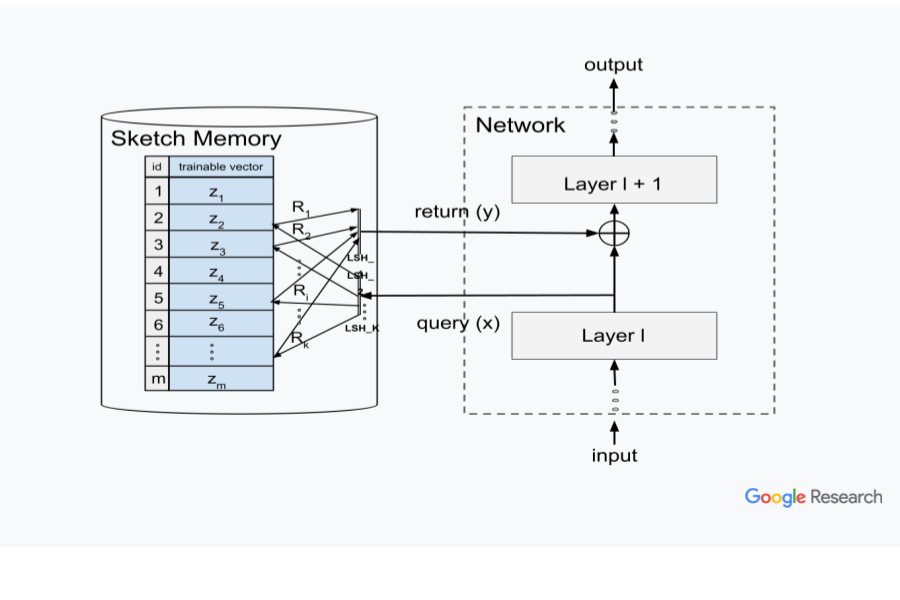
Deep learning has shown tremendous success on a variety of problems. However, unlike traditional computational paradigm, most neural networks do not have access to a memory, which might be hampering its ability to scale to large data structures such as graphs, lookup-tables, databases. We propose a neural architecture where sketch based memory is integrated into a neural network in a uniform manner at every layer. This architecture supplements a neural layer by information accessed from the memory before feeding it to the next layer, thereby significantly expanding the capacity of the network to solve larger problem instances. We show theoretically that problems involving key-value lookup that are traditionally stored in standard databases can now be solved using neural networks augmented by our memory architecture. We also show that our memory layer can be viewed as a kernel function. We show benefits on diverse problems such as long tail image classification, language model, large graph multi hop traversal, etc. arguing that they are all build upon the classical key-value lookup problem (or the variant where the keys may be fuzzy).

We present a novel attention-based model for discrete event data to capture complex non-linear temporal dependence structures. We borrow the idea from the attention mechanism and incorporate it into the point processes' conditional intensity function. We further introduce a novel score function using Fourier kernel embedding, whose spectrum is represented using neural networks, which drastically differs from the traditional dot-product kernel and can capture a more complex similarity structure. We establish our approach's theoretical properties and demonstrate our approach's competitive performance compared to the state-of-the-art for synthetic and real data.

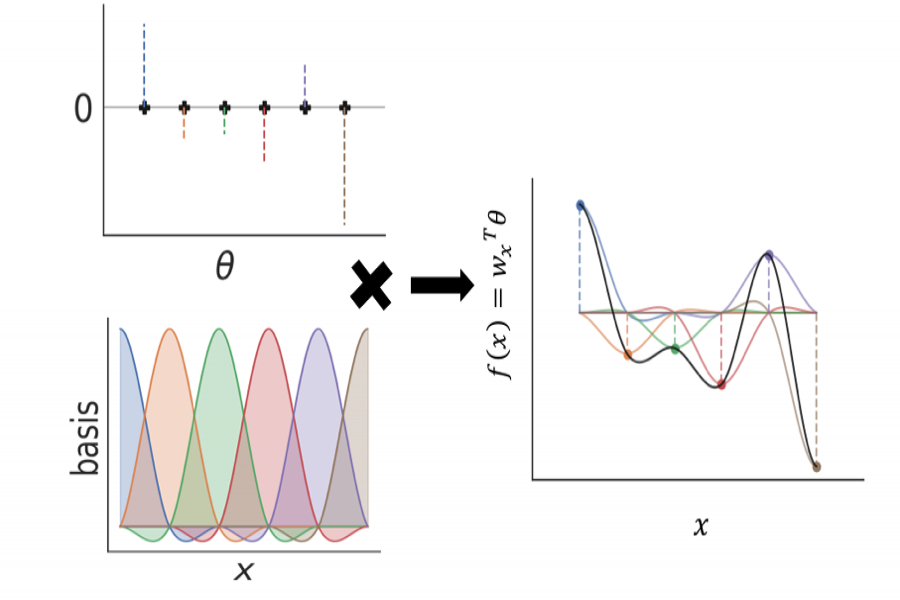
A key challenge in scaling Gaussian Process (GP) regression to massive datasets is that exact inference requires computation with a dense n × n kernel matrix, where n is the number of data points. Significant work focuses on approximating the kernel matrix via interpolation using a smaller set of m “inducing points”. Structured kernel interpolation (SKI) is among the most scalable methods: by placing inducing points on a dense grid and using structured matrix algebra, SKI achieves per-iteration time of O(n + m log m) for approximate inference. This linear scaling in n enables approximate inference for very large data sets; however, the cost is per-iteration, which remains a limitation for extremely large n. We show that the SKI per-iteration time can be reduced to O(m log m) after a single O(n) time precomputation step by reframing SKI as solving a natural Bayesian linear regression problem with a fixed set of m compact basis functions. For a fixed grid, our new method scales to truly massive data sets: after the initial linear time pass, all subsequent computations are independent of n. We demonstrate speedups in practice for a wide range of m and n and for all the main GP …